サンプルサイズの決め方
サンプリング誤差
アンケートの調査結果の精度をどの程度にするかを基準にサンプルサイズを決める方法があります。たとえば、ある通リを歩いている人100人の性別をカウントしたところ40人(40%)が女性だったとします。しかし、次の100人をカウントしても必ずしも40人ピッタリが女性とはかぎりません。34人かもしれないし45人かもしれません。この誤差をサンプリング誤差と呼び、この値が小さければ小さいほど調査結果の精度が高いといえます。
サンプルサイズを算出する方法
実際に調査を行う際に、どの程度までサンプリング誤差を許すのか誤差の範囲を事前に決めて、その誤差範囲に収めるのに必要なサンプルサイズを算出する方法があります。ここでは、この許せる誤差範囲のことを最大許容範囲と呼びます。この最大許容範囲を2で割った値を精度といいます。また、この最大許容範囲がどの程度の確率で信頼できるものであるか計る物差しを信頼度と呼びます。例えば、「信頼度95%」とは、100回調査を繰り返すと5回は間違った結果(結果が最大許容範囲からはずれる)になる可能性がある」という意味になります。「信頼度95%で最大許容範囲は、±4%以内」とは、「95%の的中率でサンプリング誤差は、±4%以内に収まる」ということになります。
数式
サンプリング誤差は以下の式で算出されます。

サンプルサイズの早見表
下の表は、この式をもとに信頼度95%のときのサンプリング誤差と母集団比率、サンプルサイズの関係を表した早見表です。(画像クリックで拡大)
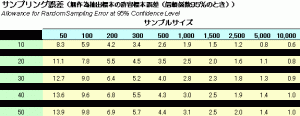
入力例を例にとると、ネットユーザー600人のうちオンラインショッピング経験という特性をもつ人が400人いたわけですから、母集団比率は400/600≒67%≒70%になります。下の表では70%の行がありませんが、50%を超えるときは100からその割合を引いた値で考えます。100-70で30%の行を見ます。サンプリング誤差が4.0%ではサンプルサイズ500人、2.8%では1,000人必要になることがわかると思います。
この早見表のデータをグラフにするとサンプリング誤差(調査結果の精度)とサンプルサイズの関係がよくわかります。サンプリング誤差を小さくするにはサンプルサイズを大きくする必要があることがよくわかります。また、単に誤差を半分にするにはサイズを倍にすればよいというものでもないことがわかります。
例)母集団比率15%のとき
サンプリング誤差7.0%→4.0%にするにはサンプルサイズ100→300ですが、
サンプリング誤差1.0%→0.3%にするのにサンプルサイズ5,000→10,000必要になります。サンプリング誤差が小さくなるからといった理由だけでサンプルサイズを5,000から10,000にするのはあまり現実的なことではありません。
関連記事:
サンプルサイズを決定するプログラム